Optimal Transport and Perfect Matching

Why is this important?

The main reason I decided to look into matching algorithms is because of their value in finding the minimal cost in machine learning. This is extremely important because we can use these algorithm to compare distributions of data by posing it as a matching problem. In machine learning, this might be useful for calculating how well a model performs by comparing the Wasserstein distances between the performance on sample distribution and the full distribution.

What is a perfect matching:

A perfect matching is a graph where every vertex is matched to another vertex such that all vertices are covered with a single edge

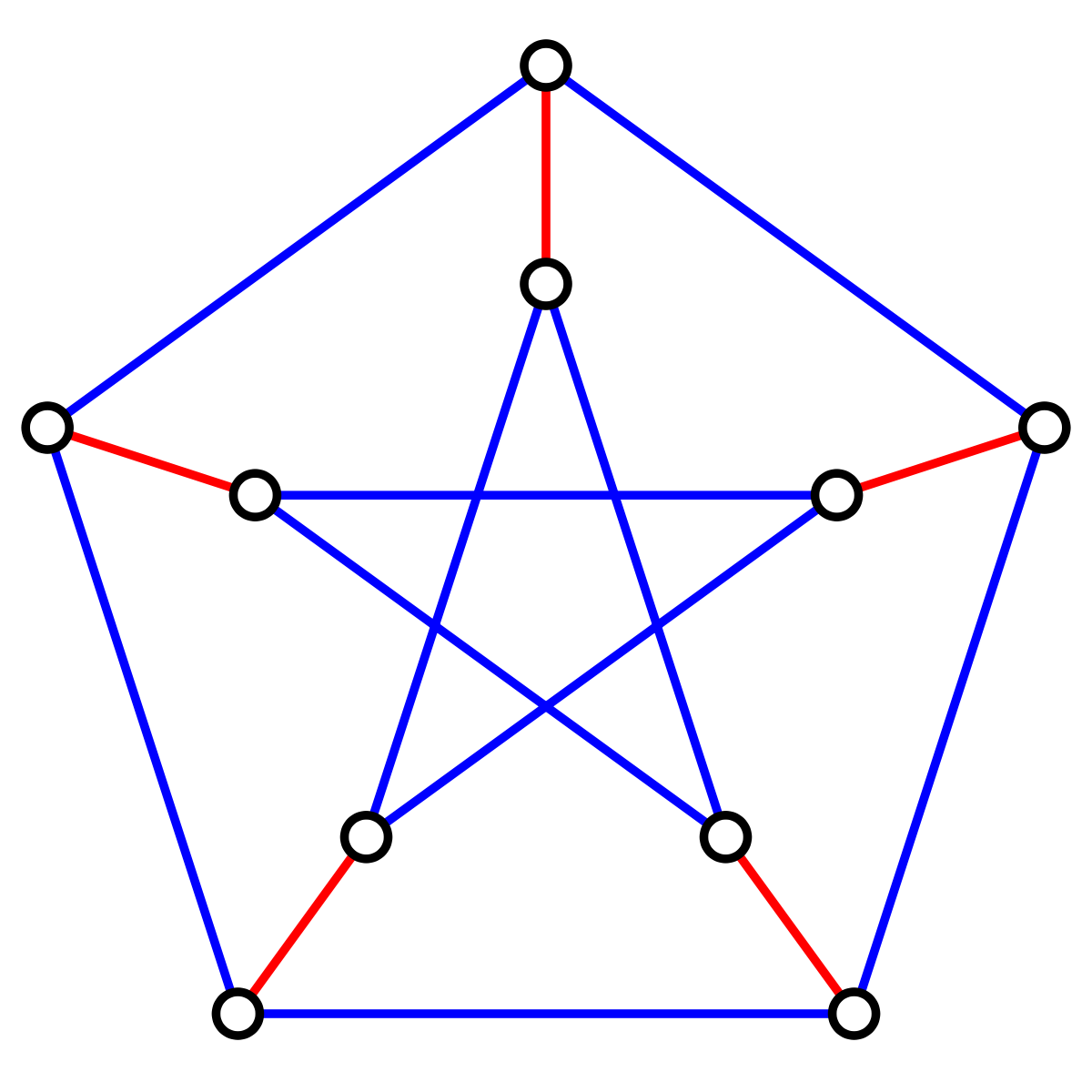
How can we find perfect matchings?

Push-Relabel Algorithm:

We have dual weights for each vertex to maintain some invariants.

We have this function

$C^P_{vw} = C_{vw} - p(v) - p(w)$ where

• $C^P$ is the reduced cost
• $p(x)$ is the dual weight for vertex x
• $u$ and $v$ are edges

Invariants:

1. all reduced costs $\geq$ 0
2. Every $e \in M$ is tight $(C_{vp}, C^P_{e} = 0)$

Theorem: If graph M is perfect and the invariants hold, the M is minimal cost

With this theorem we get the following linear program:

$\sum_{e \in C \cap M}C_e = \sum_{e \in C \cap M}C^P_e + \sum_{v \in C}p(v)$

$\sum_{e \in C - M}C_e = \sum_{e \in C - M}C^P_e + \sum_{v \in C}p(v)$

We can now iteratively solve for the minimal cost with a slack variable $\epsilon$

Application and WGAN

Earth movers Distance

$\underset{\gamma}{inf} \space \mathbb{E} |(x - y)|$

$\gamma = \pi (P, Q)$

Constraints on marginals

$\sum y(x, y) = P_r(u)$

Problem with original GAN architecture is due to the use of KL-Divergence fails to compute distances when the two distribution or non-overlapping. WGAN addresses this by using Earth mover's Distance.

Transport Plan

$EMD(P_r, P_{\theta}) = \inf || x - y || \gamma(x,y) = \inf \mathbb{E}_{x, y \in \gamma} || x - y||$

We can derive the dual formulation of EMD, by making this a maximization instead of a minimization

$EMD(P_r, P_\theta) \approx \sup_{\|f\|_L \leq 1} \left( \mathbb{E}_{x \sim P_r}[f(x)] - \mathbb{E}_{y \sim P_\theta}[f(y)] \right)$

which satisfies $|f(x_1) - f(x_2)| \leq |x_1 - x_2|$ for all $(x_1, x_2)$. This 1-Lipschitz condition ensures there is smoothness between two distributions on the discriminator corresponding to $\mathbb{E}_{p_r}[f(x)]$

To ensure Lipschitz condition on a neural net we bound the weights by clipping them then the slope can't be bigger the magnitude of the clipping.

Wasserstein GAN uses this dual formulation of Earth Mover's Distance

$min_G max_D [\mathbb{E}_{x \sim p_{data}}D(x) - \mathbb{E}_{z \sim p}D(G(z))]$

The main difference between Wasserstein GAN and regular GAN objectives is that it uses linear activation instead of sigmoid in the discriminator and removes the logs