Learning Latent Embeddings

Contrastive Learning

Contrastive Learning is the most commonly used technique to train large embedding models with transformers.

The goal of contrastive learning is to learn dense vector representations of the input modality (e.g. images, text, video) where distances between similar items are close and dissimilar items are far apart.

Siamese Networks

First introduced in Bromsky et al. as a way to perform signature verification, the Siamese Network is a neural network architecture that makes use of two towers or encoders to learn representations between similar and dissimilar items.

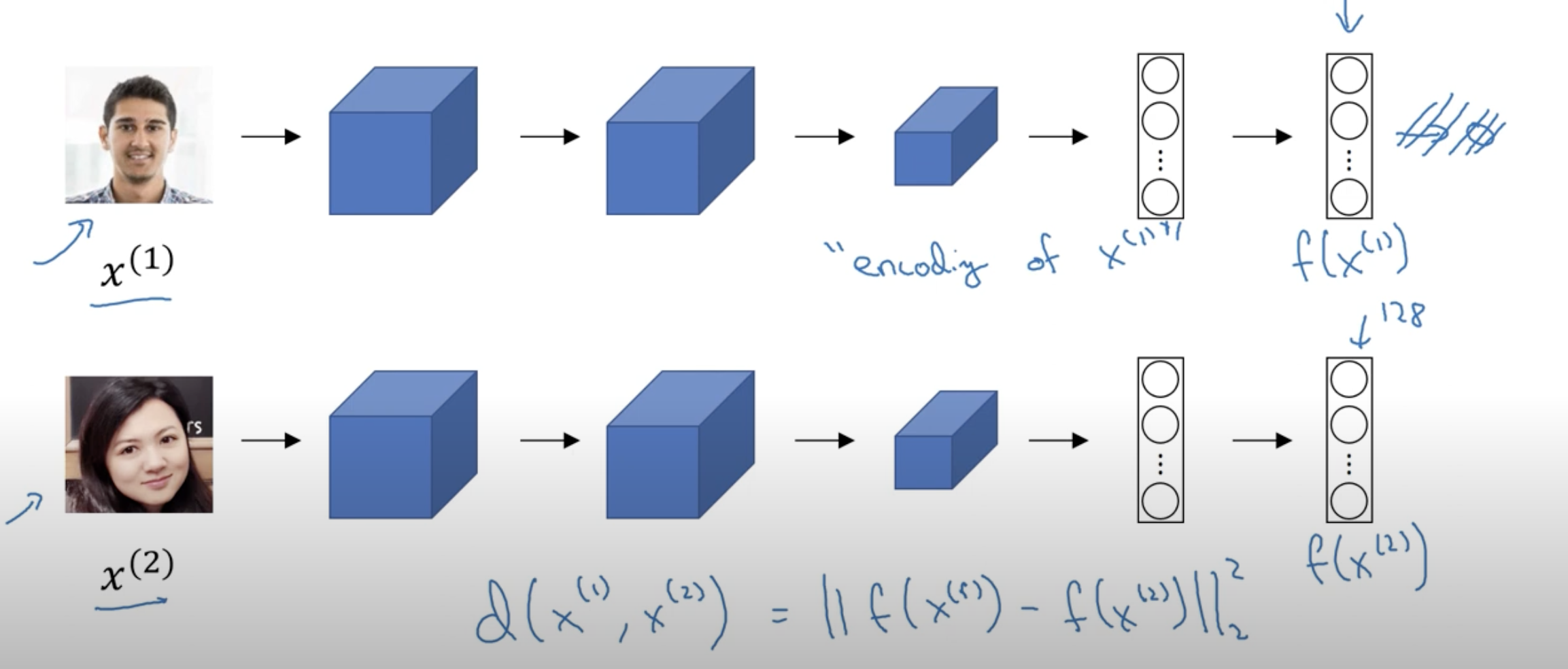
It does this by minimizing the objective $||f(x^i) - f(x^j)||^2$ when the input images $x$ are the same and maximizing the objective when they are different.

Contrastive Loss

We can formulate a loss objective where we define the similarity as the dot product of the L2-normalized feature representations.

Given that x is our query or $x^+$ and $x^-$ is our in-batch positives and negatives.

Our loss is defined as:

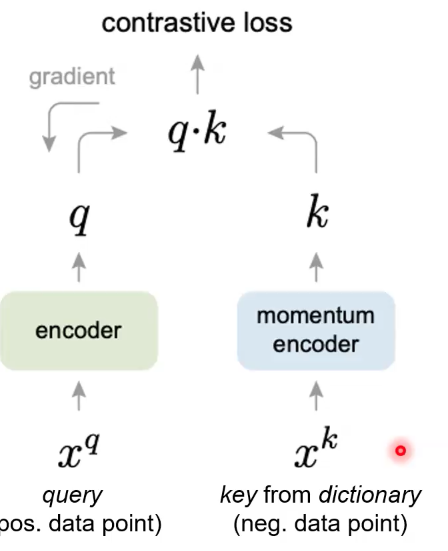
One of the first papers to explore this idea of contrastive learning for image embeddings was Momentum Encoder or MoCo (He et al. 2019)

The key takeaway from MoCo was that it makes use of a dummy encoder from which resolves the computational cost of training a unique encoder without losing quality of negative encodings over time.

Triplet Loss

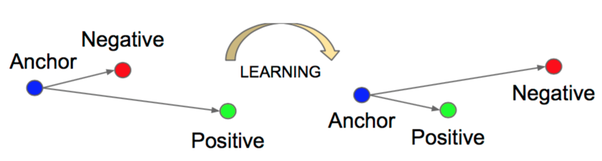
Triplet loss can be viewed as a better contrastive loss. Given an anchor $A$, a positive sample $P$, and a negative sample $N$, Triplet seeks to minimize the objective

$l(A,P,N) = \max((|f(A)-f(P)|)^2 - (|f(N)-f(A)|)^2 + \alpha, 0)$

where each absolute value term represents the distance between the encodings learned of anchor A and the negative and positive samples.

We want to make sure $(|f(A)-f(P)|)^2 - (|f(N)-f(A)|)^2$ or the distance between the anchor and positive term is less than the distance between the anchor and the negative term. Additionally, sometimes we have threshhold $\alpha$ to ensure that the model learns that positives and anchors are much more similar than negatives and anchors.

Relationship with Language Modeling

Computing a vector similarity between latent vectors to extract meaning behind the data is reminiscent to the core principle behind self-attention in language models such as GPT (Generative Pre-Trained Transformer)

From the diagram below, a transformer learns through self-attention the similarity level between different words or tokens in the input dictionary.

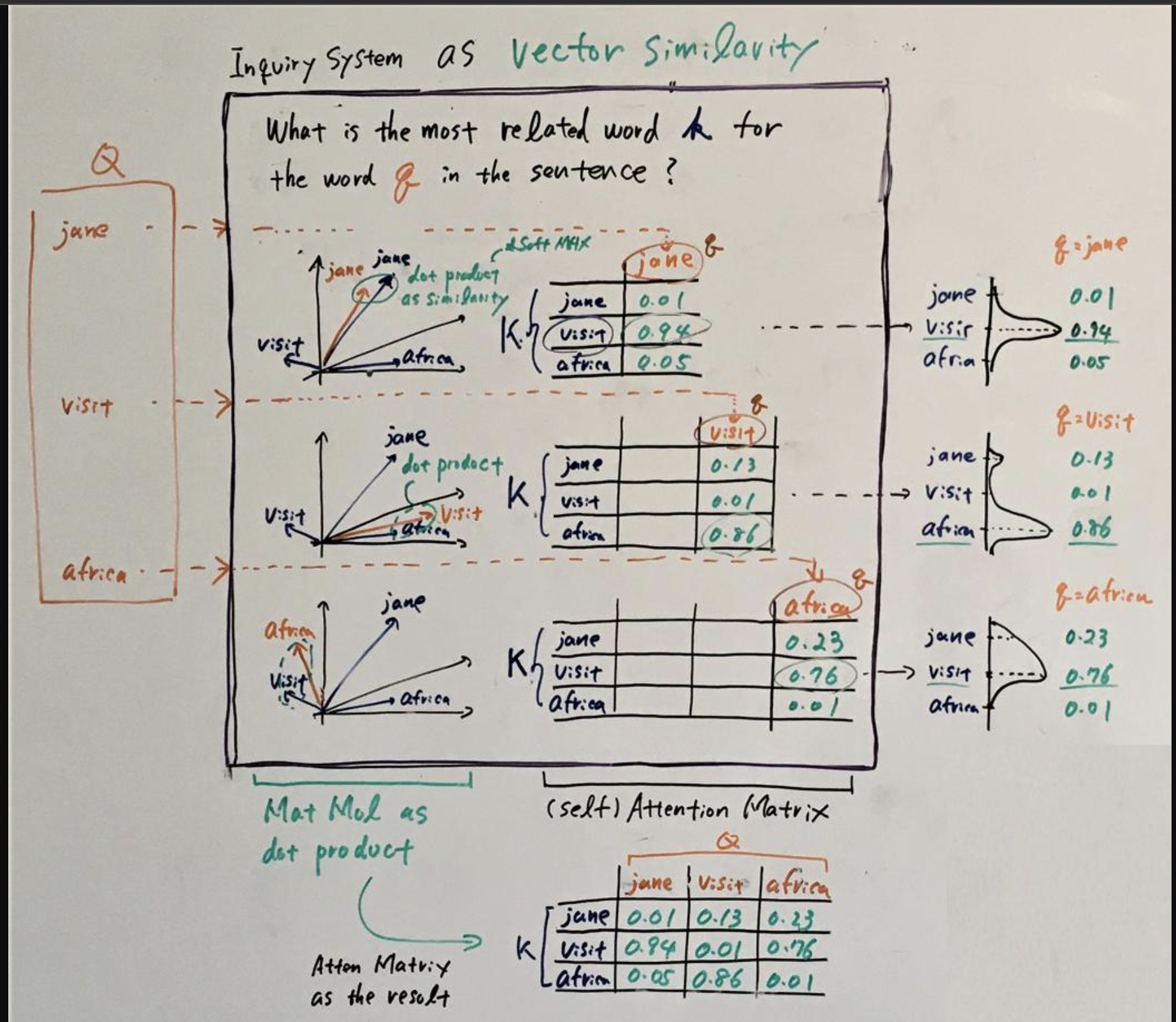
When we generate new words, the model selects the word with the highest probability in relation to the query and keys computed by a weighted similarity or attention function $softmax(\frac{QK^T}{\sqrt{d_k}})V$.

More specifically, this computation is represented by a lookup table defined by learnable parameters from our word embedding $x_i$ and our encoder networks $Q$, $K$, and $V$.

$q_i = Qx_i \text{ (queries) } \quad k_i = Kx_i \text{ (keys) } \quad v_i = Vx_i \text{ (values)}$

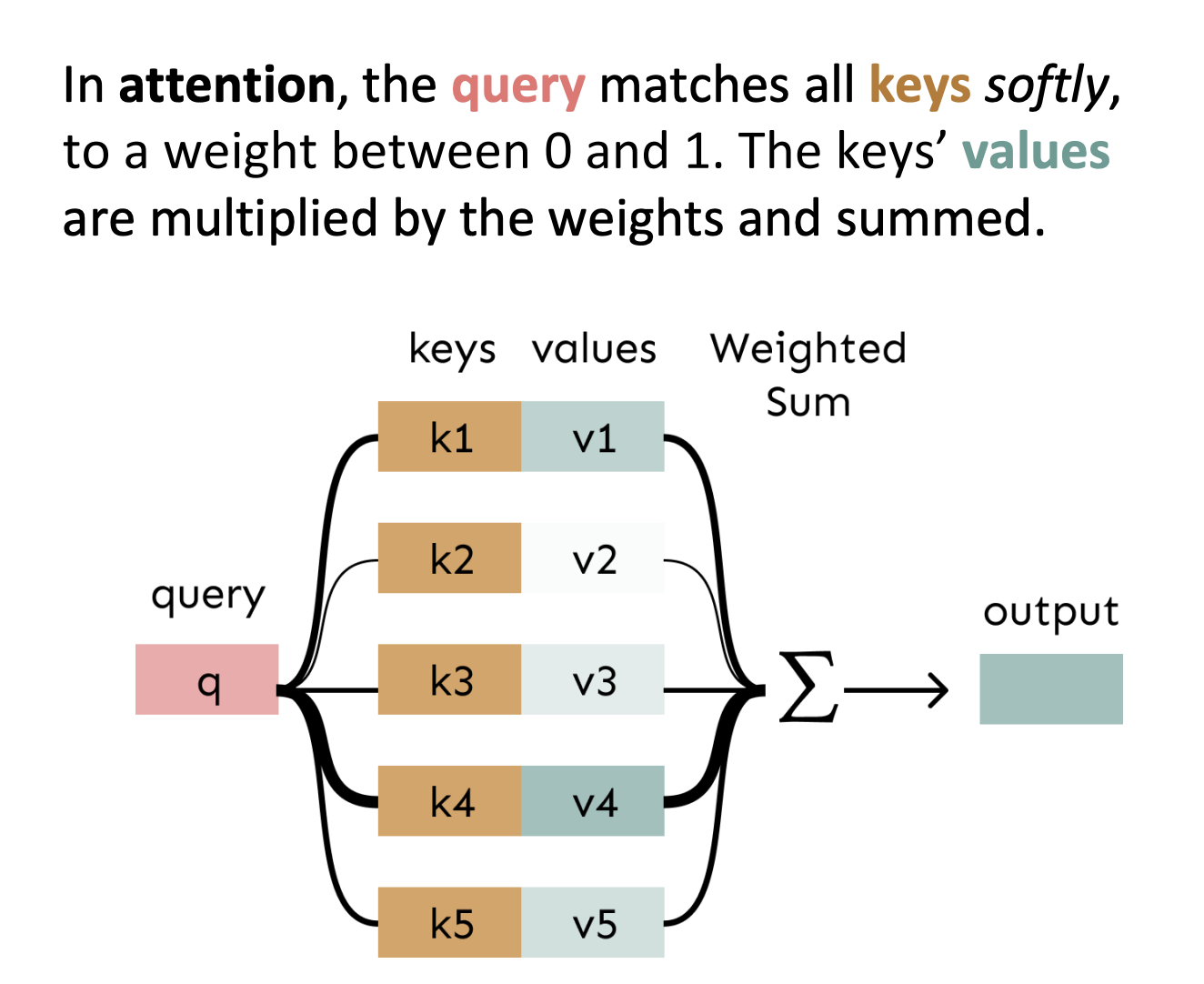
High-level overview

At a high level, a transformer is learning an implicit probability transition matrix based off of predicting the next term from the context. This can be formalized in multi-headed attention like so:

$p(x_t | x_{t-1} ... x_{1}) = softmax(FFN_n(max(0, (Norm(Concat(h_1, h_2, ... , h_k) W^0 )))))$

where an attention head $h_i$ is computing the function

$h_i = softmax(\frac{QK^T}{\sqrt{d_k}})V$

with a multi-layer feed forward network defined as:

$FFN_i(x) = max(0, W_{i-1}(FFN_{i-1}(x) + b))W_i + b$

Dimensionality Reduction

Understanding the nature of the high-dimensional representations your model is learning can seem overly abstract especially when working with vectors of size 1000 and greater.

Fortunately, there exist dimensionality reduction techniques to visualize and understand these embeddings. One commonly used technique for dimensionality reduction of embeddings is UMAP (Uniform Manifold Approximation and Projection).

The core idea of UMAP is to find a global topological structure of the data. More on this here.

Below is an example of how UMAP can represent text embeddings of different internet content you might see in your "For You Page" in 3D.

Conclusion

Thanks for reading up to this point!

Hopefully, you learned a little about representation learning and gained some intuition on how DL models learn semantic relationships through encoding latents.

Acknowledgements

Thank you to Andrew Zhang for feedback on earlier drafts!

Resources

• C4W4L03 Siamese Network
• Momentum Encoder
• C4W4L04 Triplet loss
• CS480/680 Lecture 19: Attention and Transformer Networks
• Stanford CS224N NLP with Deep Learning | 2023 | Lecture 8 - Self-Attention and Transformers
• What exactly are the Keys, Values, and Queries in a Transformer?